 |
(6.16) |

| turbulenter Massendiffusionsparameter, | |
| Wirbelviskosität und | |
| turbulente SCHMIDT-Zahl. |
| Energieverbrauch durch Dichteschichtung (Buoyancy) und | |
| Dissipation. |
| turbulente FROUDE-Zahl, | |
| charakteristische Geschwindigkeit der Turbulenz, | |
| Makro-Länge, | |
| BRUNT-VÄISÄLÄÄ Frequenz Gl. (6.8), |
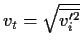 und steht dadurch im engen Bezug zur turbulenten kinetischen Energie, s.
Gl. (7.6).
Die Herleitung der Makro-Länge
und steht dadurch im engen Bezug zur turbulenten kinetischen Energie, s.
Gl. (7.6).
Die Herleitung der Makro-Länge | kinematische Viskosität. |