folgt: 7.3 Stabilitätsfunktion hinauf: 7. Turbulenzmodell vorher: 7.1 Grundgleichungen

7.2 Staupunkt-Anomalie

Das Phänomen, dass bei Berechnungen mit dem k-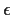-Modell in Staupunkten unnatürlich hohe Werte der kinetischen Energie k der Turbulenz auftreten, wird von KATO und LAUNDER [57] beschrieben. Selbige Autoren schlagen an gleicher Stelle eine Modifikation des Produktionsterms in Gl.(7.1) vor. Die Ursache des Phänomens lässt sich folgendermaßen beschreiben: Im Vorgriff auf das in Abschnitt 9.2.3 angegebene Geschwindigkeitsfeld ergibt sich für eine Potential-Staupunktströmung Gl.(9.3) folgender Geschwindigkeitsgradienten-Tensor:

$$\frac{\partial \overline{v_i}}{\partial x_j}= \left(\begin{a... ... a & 0 & 0 \\ 0 & -a & 0 \\ 0 & 0 & 0 \end{array}\right)$$ (7.11)

mit

a	Konstante.

Der REYNOLDS-Spannungstensor ergibt sich daraus gemäß Gl. (7.3) wie folgt:

$$-\overline{ v_{i}^{\prime} v_{j}^{\prime}}= \left(\begin{arr... ...\frac{2}{3}k & 0 \\ 0 & 0 & -\frac{2}{3}k \end{array}\right)$$ (7.12)

Damit ergibt sich für die Produktion, s. Term 3 in Gl. (6.15):

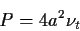$$P= 4 a^2 \nu_{t}$$ (7.13)

Mit dem Ansatz für die Wirbelviskosiät 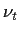, s. Gl. (7.4), wird daraus:

$$P= 4 a^2 c_{\mu} \frac{k^2}{\epsilon}$$ (7.14)

Die Produktion steigt also mit zunehmendem k quadratisch. Dies erklärt den rapiden Anstieg der kinetischen Energie k der Turbulenz, der entgegen experimenteller Erkenntnis [57] vom k-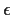-Modell erzeugt wird. Bei näherer Betrachtung fällt auf, dass im Spannungstensor Gl. (7.12) die Normalspannungen ungleich groß (anisotrop) sind und dass bei genügend großem a die 11-Normalspannung auch positiv werden kann (Zug statt Druck). Widersprüchlich ist daran, dass die Korrelation 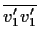niemals kleiner als Null werden kann. Unplausibel ist, dass das k-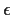-Modell, das zur Schließung drei skalare Größen k, 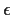und 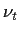verwendet, brauchbare Informationen über die Anisotropie der Normalspannungen liefern könnte.

Der Ansatz für die REYNOLDS-Spannungen Gl. (7.3) entspricht dem Materialgesetz für inkompressible NEWTON-Fluide [110]. Dabei entspricht dem Druck p und die Wirbelviskosität 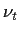der molekularen Viskosität 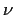. Die Anisotropie der Normalspannungen taucht demnach auch in laminaren Strömungen viskoser NEWTON-Fluide auf. In den NAVIER-STOKES-Gleichungen für inkompressible NEWTON-Fluide üben die Diagonalkomponenten des Geschwindigkeitsgradienten, welche die Normalkomponenten im Spannungstensor hervorrufen, keine Wirkung aus, da sich der Zähigkeitsterm nach [110] in 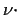rot(rot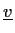) umformen lässt. Die Frage, ob eine Anisotropie der Normalspannungen in inkompressiblen NEWTON-Fluiden auftritt, ist somit irrelevant. Erst der Produktionsterm in der Gleichung für die kinetische Energie k der Turbulenz (Gl. (6.15)) in Verbindung mit dem Wirbelviskositätsansatz nach Gl. (7.3) zwingt zur Beschäftigung mit dieser Frage.

Wenn das zeitlich gemittelte Geschwindigkeitsfeld einer Strömung rotationsfrei ist, dann ist der Gradiententensor von diesem Geschwindigkeitsfeld symmetrisch. Ein solcher Geschwindigkeitsgradienten-Tensor lässt sich auf orthogonale Hauptachsen transformieren, so dass der Tensor im transformierten Koordinatensystem nur noch auf der Diagonalen besetzt ist. Man muss nun annehmen, dass in diesem transformierten Hauptachsensystem die Diagonalkomponenten des REYNOLDS-Spannungstensors - 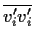gleich groß (isotrop) sind, damit in inkompressiblen Fluiden die Produktion von k verschwindet. Ohne Produktion klingt die Turbulenz ab.

KATO und LAUNDER [57] modifizieren den Ansatz für den Produktionsterm, s. Term 3 in Gl. (6.15). Zunächst einmal lässt sich der Geschwindigkeitsgradient in einen symmetrischen und einen antisymmetrischen Teil 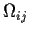aufspalten:

$$\frac{\partial \overline{v_i}}{\partial x_j}= S_{ij} + \Omega_{ij}$$ (7.15)

mit

$$S_{ij} = \frac{1}{2}\left( \frac{\partial \overline{v_i}}{\partial x_j}+ \frac{\partial \overline{v_j}}{\partial x_i} \right)$$ (7.16)

und

$$\Omega_{ij} = \frac{1}{2}\left( \frac{\partial \overline{v_i... ...ial x_j}- \frac{\partial \overline{v_j}}{\partial x_i} \right)$$ (7.17)

KATO und LAUNDER [57] machen den folgenden Ansatz für die Produktion:

$$P= c_{\mu}\frac{k^2}{\epsilon}2\sqrt{ S_{ij} S_{ij}} \sqrt{\Omega_{ij} \Omega_{ij}}$$ (7.18)

In einer rotationsfreien Strömung sind alle Komponenten von . Die KATO-LAUNDER-Modifikation führt also dazu, dass in Potentialströmungen die Produktion in jedem Fall verschwindet und nicht nur dann, wenn die o.g. Isotropie im transformierten Hauptachsensystem gegeben ist.

Wenn das Fluid sich im zeitlichen Mittel wie ein starrer Körper bewegt, die Geschwindigkeiten also als Kombination einer Translation und einer Rotation darstellbar sind, findet sowohl bei der KATO-LAUNDER-Modifikation als auch im Standard-Modell keine Produktion von Turbulenz statt.

Desweiteren ergibt sich in beiden Formulierungen dieselbe Produktion, wenn nur eine Nebendiagonalkomponente des Geschwindigkeitsgradienten auftritt, wie dies z. B. in den Testrechungen von Abschnitt 9.3.3 und 9.3.4 der Fall ist. folgt: 7.3 Stabilitätsfunktion hinauf: 7. Turbulenzmodell vorher: 7.1 Grundgleichungen