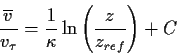 |
(2.1) |
| zeitlich gemittelte Geschwindigkeit in Längsrichtung , | |
| Schubspannungsgeschwindigkeit
|
|
| Wandschubspannung , | |
| Dichte , | |
| KARMAN-Konstante , | |
| Wandabstand (von der Sohle aufwärts) , | |
| Referenzabstand, s.u. und | |
| Konstante . |
| äquivalente Sandrauheit nach NIKURADSE. |
| kinematische Viskosität. |
| Turbulente Schubspannung und | |
| Wirbelviskosität . |
| Mischungsweglänge . |
| Wassertiefe |
 |
(2.9) |
| Wandabstand des sohlnächsten Diskretisierungspunkts und | |
| CHEZY-Koeffizient . |