folgt: 12. Anhang
hinauf: Turbulenzmodellierung für stabil dichtegeschichtete
vorher: 10.3 Ausblick
11. Zusammenfassung
In Flussmündungen (Ästuaren) mit genügend großem Tidehub bilden sich
Trübungszonen aus.
In diesen werden große Mengen kohäsiver Sedimente im Wechsel der
Tidebewegung erodiert, in suspendierter Form vom Wasser mitgeführt und wieder
deponiert. Die vom Menschen geschaffenen Einrichtungen wie Häfen und
Fahrrinnen sind im Bereich der Trübungszonen ständig von Verschlickung
bedroht. Die numerische Simulation des Transports kohäsiver Sedimente ist
bisher nur mit eingeschränkter Genauigkeit möglich.
Diese Arbeit leistet einen Beitrag dazu, die Differenzen zwischen Realität und
numerischer Berechnung zu quantifizieren.
In Besonderheit wird der Frage nachgegangen, welchen Anteil das Turbulenzmodell
als eines von vier empirischen Ansätzen an o. g. Differenzen hat.
Die Überprüfung der Turbulenzmodellierung findet am Beispiel des
k-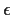 -Modells statt.
Als praxisrelevantes Maß für die Abweichungen wird der Massenstrom des
Sediments benutzt.
-Modells statt.
Als praxisrelevantes Maß für die Abweichungen wird der Massenstrom des
Sediments benutzt.
Typischerweise treten im Wasser von Ästuaren Dichteunterschiede auf, die durch
unterschiedliche Konzentrationen von suspendiertem Sediment und gelöstem Salz
verursacht werden.
Die Dichteschichtung ist dabei in aller Regel stabil,
d. h. die Dichte nimmt nach unten hin zu, da das Salzwasser
das Süßwasser unterläuft, und das Sediment von oben nach unten sinkt.
Auf die Turbulenz wirkt eine stabile Dichteschichtung dämpfend, da die Vermischung
der Konzentrationsunterschiede potentielle Energie verbraucht.
Die Berücksichtigung dieser Dämpfung ist bei der Berechnung der turbulenten
Vermischung entscheidend. Eine begründete Vermutung besagt, dass die von
kohäsiven Sedimenten ausgelöste Dichteschichtung die Turbulenz in bestimmten
ästuarinen Strömungen sogar vollständig zum Verlöschen bringen kann.
Im Rahmen dieser Arbeit ist die Strömungsberechnungs-Software ,,casu``
programmiert worden. Unter Verwendung der hydrostatischen Druckannahme werden
alle drei Raumdimensionen diskretisiert. Damit lassen sich Strömungen in
flachen Gewässern mit freier Oberfläche simulieren. Der finite Volumen Ansatz
für die Kontinuitätsgleichung ermöglicht eine exakte Erfüllung der
Massenbilanz.
Die Stromlinienrückverfolgung zur Erfassung der Konvektion
ermöglicht es, das ansonsten explizite Verfahren auch bei COURANT-Zahlen über
Eins zu verwenden.
Der auf Literaturvorschlägen basierende
numerische Algorithmus wurde hier um die Möglichkeit der Verwendung
unstrukturierter Gitter und um das Turbulenzmodell erweitert.
Mit der Software ,,casu`` sind Testrechnungen durchgeführt worden, die zunächst
einmal die Funktion des Basismodells überprüft haben.
Daran anschließend ist die Implementierung des Turbulenzmodells
erprobt worden. Durch Vergleich mit analytischen Lösungen kann die
Funktionsfähigkeit aller Terme des Turbulenzmodells dargelegt werden. Durch
Vergleich mit Experimenten gelingt die Bestimmung der Modellkonstanten des
Turbulenzmodells. Dies führt auf die Überlegung, statt mit festen Werten für
die Modellkonstanten mit Wertespannen zu arbeiten. Diese Wertespannen könnten
über den Weg einer Sensitivitätsuntersuchung auch in der praktischen
Berechnungstätigkeit einen Zugriff auf die Modellungenauigkeiten ermöglichen.
Turbulenzdämpfung in stabil dichtegeschichteten Fluiden wurde am Beispiel der
Gleichdruck-Wandgrenzschicht und der freien ebenen Scherschicht erprobt.
Es zeigt sich, dass die Wandgrenzschicht durch die Hinzunahme einer
Stabilitätsfunktion genauer berechnet werden kann. Die ebene Scherschicht
lässt sich durch Veränderung der experimentellen Randbedingungen so stark
beeinflussen, dass aus dem Vergleich zwischen Experiment und Berechnung nur
auf eine qualitative Übereinstimmung geschlossen werden kann. Genauere
Aufschlüsse bezüglich freier Scherschichten wären nur durch Vergleich mit
Experimenten möglich, in denen praxisrelevantere Randbedingungen verwendet
werden.
Mit dem absinkenden Sediment werden zwei für das Ästuar typische Situationen
berechnet. Bei großer Strömungsgeschwindigkeit wird das Sediment erodiert und
verursacht eine Dichteschichtung in Bodennähe. Es werden die
Ergebnisse der Berechnung mit dem Standard k-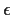 -Modell mit denjenigen
verglichen, die durch Hinzunahme der Stabilitätsfunktion erzielt worden sind.
Die Stabilitätsfunktion erlaubt es, in dieser Situation die Realität
genauer zu approximieren.
Das Standard
k-
-Modell mit denjenigen
verglichen, die durch Hinzunahme der Stabilitätsfunktion erzielt worden sind.
Die Stabilitätsfunktion erlaubt es, in dieser Situation die Realität
genauer zu approximieren.
Das Standard
k-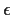 -Modell berechnet eine Sohlschubspannung, die 15% größer ist.
Durch Einsetzen in ein gängiges Erosionsmodell ergibt sich ein um 42%
größerer Massenstrom.
-Modell berechnet eine Sohlschubspannung, die 15% größer ist.
Durch Einsetzen in ein gängiges Erosionsmodell ergibt sich ein um 42%
größerer Massenstrom.
Als zweiter Testfall mit absinkendem Sediment wird eine Konfiguration
verwendet, bei der im Ästuar typischerweise Sediment deponiert wird. Die
Berechnung zeigt, dass in diesem Fall neben einem Abklingen der Turbulenz
infolge des absinkenden Sediments ein instationäres, vom Boden ausgehendes
Wieder-Aufflackern der Turbulenz mit einer Periodendauer in der Größenordnung
des Tidezyklus stattfindet. Strömungen, die Sediment deponieren, können
also nicht mit stationären Gerinneströmungen verglichen werden.
Des Weiteren lässt sich damit erkären, warum Deposition kein gleichmäßiger
sondern ein episodischer Vorgang ist.
folgt: 12. Anhang
hinauf: Turbulenzmodellierung für stabil dichtegeschichtete
vorher: 10.3 Ausblick
Jens WYRWA * 2003-11-05