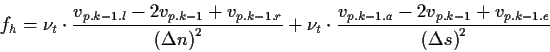 |
(8.8) |
| Wirbelviskosität, | |
| Geschwindigkeit auf der Kantenmitte, | |
|
|
Geschwindigkeiten links und rechts neben der Kante, |
|
|
Geschwindigkeiten am Anfang und am Ende der Kante, |
| Ortsschrittweite quer zur Kante, | |
| Kantenlänge, Ortsschrittweite längs zur Kante, | |
| Indizes | |
| p | parallel zur Kantenrichtung und |
| k-1 | vorangegangener Zeitschritt. |
| Dicke der mitgezogenen Fluidschicht, | |
| d. h. Wandabstand bei dem
|
|
| Viskosität und | |
| t | Zeitdauer seit Beginn der Wandbewegung. |