| v |
Geschwindigkeit, |
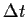 |
Zeitschrittweite, |
| g |
Fallbeschleunigung, |
| z |
geodätische Höhe, |
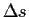 |
Kantenlänge, Ortsschrittweite, |
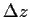 |
Schichtdicke, |
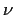 |
Wirbelviskosität an der Unterseite der indizierten Schicht, |
| f |
Reibung, f friction, |
| b |
Einfluss der variablen Dichte, b buoyancy, |
| Indizes |
|
| p, n |
Geschwindigkeitskomponente parallel bzw. normal |
| |
zur Kantenrichtung, |
| k, k-1 |
aktueller Zeitschritt, vorangegangener Zeitschritt, |
| j |
Nummerierung der jeweiligen Schicht 1...M, |
| u |
Größe am Ursprung der Bahnlinie, |
| s |
Wasserspiegelhöhe, s surface, |
| a, e |
Knoten am Anfang bzw. am Ende der Kante und |
| h |
horizontal. |