folgt: 8.4 Entwicklungsmöglichkeiten hinauf: 8.3 Verfahrenserweiterung vorher: 8.3.1 Unstrukturierte Netze

8.3.2 Stofftransport und Turbulenzmodell

CASULLI [17] erwähnt die Hinzunahme der Dichte in sein Verfahren und zeigt auch Berechnungsergebnisse. Jedoch fehlen Angaben zu den Details des implementierten Algorithmus.

Im Programm ,,casu`` werden die Konzentrationen und die Turbulenzgrößen in ähnlicher Weise behandelt, weshalb der vorliegende Abschnitt sowohl den numerischen Algorithmus für die Lösung der Stofftransportgleichungen als auch denjenigen zur Berechnung der Turbulenzgößen des k-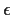-Modells beschreibt. Die Berechnung erfolgt im jeweiligen Zeitschritt, nachdem das Strömungsfeld (Lage des Wasserspiegels und mittlere Geschwindigkeiten) berechnet worden ist.

Alle Konzentrationen und die aus ihnen resultierende Dichte werden an den Schnittpunkten der Knoten-Vertikalen mit den horizontalen Levels diskretisiert. Die Turbulenzgrößen werden auf den Schnittpunkten der Kantenmitten-Vertikalen mit den horizontalen Rändern der Schichten diskretisiert (s. Bild 15).

Die einzelnen Terme der Stofftransport-Gl. (6.4) werden folgendermaßen diskretisiert: Die Konvektion wird mit der ELM erfasst. Die vertikale Diffusion wird analog zur Impulsdiffusion (Reibung) implizit diskretisiert. Die horizontale Diffusion wird dementsprechend explizit angesetzt. Der Term, der das Absinken des Sediments beschreibt, wird implizit diskretisiert. Der darin vorkommende vertikale Konzentrationsgradient wird mit dem darüber liegenden Konzentrationswert gebildet. Es ist im Programm ,,casu`` die Möglichkeit geschaffen worden, eine konstante Quelle für jede Konzentration vorzugeben. Die diskretisierte Form der Stofftransport-Gl. (6.4) lautet dann wie folgt:

$$\frac{c_{k.j}-c_{k-1.j.u}}{\Delta t} =$$

$$D_{k-1}\frac{c_{k.j+1}-2c_{k.j}+c_{k.j-1}}{\left(\Delta z\right)^2}$$

$$+D_{k-1}\frac{c_{k-1.j.l}-2c_{k-1.j}+c_{k-1.j.r}}{\left(\Del... ...c{c_{k-1.j.a}-2c_{k-1.j}+c_{k-1.j.e}}{\left(\Delta s\right)^2}$$

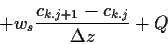$$+ w_s \frac{c_{k.j+1}-c_{k.j}}{\Delta z} + Q$$ (8.11)

mit den Indizes wie in Gl. (8.5).

Für die Berechnung der Konzentrationsverteilung im aktuellen Zeitschritt muss demnach an jeder Knoten-Vertikalen ein lineares Gleichungssystem gelöst werden.

Beim Turbulenzmodell, siehe Abschnitt 7.1, sind drei Feldgrößen miteinander verwoben: k, 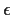und 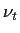. Für die Berechnung dieser gekoppelten Differentialgleichungen wird in dieser Arbeit auf einen Vorschlag von ILINCA [51] zurückgegriffen. Die Lösung der beiden Differential-Gln. (7.1) und (7.2) erfolgt dabei nacheinander. Die nichtlineare Kopplung wird durch folgendes iteratives Vorgehen berücksichtigt: Ausgehend von einer bekannten Verteilung von 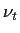wird die Differential-Gl. (7.1) für k gelöst^8.10. Die darin auftretende Dissipationsrate wird mit Hilfe der Beziehung Gl. (7.4) ersetzt. Danach kann dann die Differential-Gl. (7.2) für 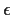gelöst werden. Damit sind k und 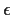bekannt. Die Beziehung Gl. (7.4) erlaubt es nun, 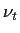erneut zu berechnen. Werden dabei relativ große Änderungen festgestellt, so beginnt die Iteration von neuem mit der Berechnung von k. Eine Rückkopplung des veränderten 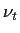mit dem Geschwindigkeitsfeld, wie sie ILINCA [51] vorschlägt, ist in dieser Arbeit nicht realisiert worden, weil in den Testberechnungen Konvergenz auch ohne eine Rückkopplung erzielt werden konnte. Die getrennte Berechnung des Strömungsfeldes und der Turbulenzgrößen sowie die Unterrelaxation der Veränderung der Turbulenzgrößen wird auch von FERZIGER und PERIC [34] als notwendig zur Erzielung von Konvergenz angesehen.

Es muss verhindert werden, dass die Turbulenzgrößen k und 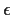negativ werden^8.11. Dazu wird das Unterschreiten eines Grenzwertes im Programm abgefragt. Falls eine Unterschreitung vorliegt, wird der Wert der Turbulenzgröße dem Grenzwert gleichgesetzt (clipping). Zur Vermeidung negativer Werte schlägt ILINCA [51] die Verwendung der Logarithmen der Turbulenzgrößen vor. Diese Möglichkeit konnte im Rahmen dieser Arbeit leider nicht bis zum Ende verfolgt werden.

Bei der o. g. numerischen Lösung der Turbulenz-Differential-Gln. (7.1) und (7.2) wird analog zur Berechnung einer Stofftransportgleichung verfahren. Die einzelnen Terme werden folgendermaßen diskretisiert: Die ELM dient zur Erfassung der Konvektion. Die vertikale Diffusion wird implizit, die horizontale Diffusion hingegen explizit angesetzt. Die implizite Berechnung der Dissipation lässt die diskretisierten Gleichungen nichtlinear werden. Diese Nichtlinearität wird in dieser Arbeit mittels einer Newton Iteration gelöst. Die Berechnung des Produktionsterms verwendet die für den aktuellen Zeitschritt bereits bekannten Geschwindigkeiten und die Turbulenzgrößen aus dem vorangegangenen Zeitschritt, ist also explizit. Der Buoyancyterm wird ebenfalls explizit diskretisiert, d. h., dass der Dichtegradient des vorangegangenen Zeitschritts benutzt wird. Die Verwendung der ELM für die Konvektion und die explizite Diskretisierung der horizontalen Diffusion führen dazu, dass implizit nur die Größen in einer Vertikalen miteinander verbunden sind. Somit können bei der Berechnung der Turbulenzgrößen alle Kantenmitten-Vertikalen einzeln nacheinander abgearbeitet werden.

Auf die Beschäftigung mit viskosen Unterschichten ist in dieser Arbeit auch aufgrund der in Abschnitt 5.5 aufgeworfenen Fragen verzichtet worden. Wo erforderlich werden die Beziehungen Gl. (9.23) und Gl. (9.24) als Sohlrandbedingungen für die Turbulenzgrößen verwendet. folgt: 8.4 Entwicklungsmöglichkeiten hinauf: 8.3 Verfahrenserweiterung vorher: 8.3.1 Unstrukturierte Netze