folgt: 10. Auswertung hinauf: 9.5 Suspendierte Sedimente vorher: 9.5.2 Erosion

9.5.3 Deposition

Um sich dem Vorgang der Deposition^9.19anzunähern, wurde in diesem Abschnitt ein Testfall berechnet, in dem der absinkende Sedimentmassenstrom denjenigen Massenstrom übertrifft, der von der Turbulenz durch Mischung nach oben befördert wird. Dazu wurde das Beispiel gewählt, in dem WINTERWERP [142] einen Turbulenzkollaps gefunden hat. In diesem Beispiel beträgt die Wassertiefe 16 m. Das Wasser hat eine tiefengemittelte Geschwindigkeit von 0,2 m/s, die durch die Vorgabe eines Wasserspiegelgefälles von 1:2,2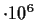, d. h. 0,92 mm in dem 2000 m langen Berechnungsgebiet erzeugt wird. Dies entspricht einer Sohlrauheit von 1,0 mm. Das zufließende Wasser hat eine konstante Sedimentkonzentration von 0,024 g/l. Die Sinkgeschwindigkeit des Sediments beträgt 0,5 mm/s. 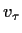Der Vorgabe des Wasserspiegelgefälles entspricht eine Schubspannungsgeschwindigkeit = 0,0085 m/s. Diese wird nun benutzt, um die Randbedingungungen für die Turbulenzgrößen k und 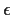festzulegen. Gemäß Gl. (9.23) und (9.24) werden die Werte an der Sohle so angesetzt, als ob sich der erste Knoten des Berechnungsgebietes in 0,030 m Abstand von der Sohle und damit bereits in der logarithmischen Schicht befindet. Am Zuströmrand wird in den unteren 1,5 m der Wassertiefe eine Verteilung gemäß Gl.(9.23) und (9.24) angesetzt. Bei Sohlabständen von mehr als 1,5 m sind die Werte k und 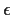konstant. Passend dazu stellt sich am Zuströmrand ein Geschwindigkeitsprofil ein, das im sohlnahen Bereich logarithmisch ist.

Bild 42a gibt die Berechnung von WINTERWERP [142] wieder, die er mit seinem 1DV-Modell^9.20erzielt hat. Die 2000 m Fließstrecke im 3D-Modell ,,casu`` entsprechen dabei den ersten 167 Minuten Berechnungszeit von WINTERWERP.

Das entscheidende Ergebnis dieses Abschnitts ist, dass unter den gegebenen Randbedingungen kein stationärer Zustand mehr auftritt, wie in Bild 42b anhand der dort gezeigten Längsschnitte der kinetischen Energie k der Turbulenz sichtbar wird. Es ist erkennbar, dass die Turbulenz im oberen Teil des Wasserkörpers abklingt. Dies ist zum einen auf die Vorgabe eines gemessen am stationären Wert der Gerinneströmung zu großen Turbulenzgrades am Zuströmrand zurückzuführen. Zum anderen baut das absinkende Sediment eine Dichteschichtung auf, die ebenfalls turbulenzdämpfend wirkt. Wenn die Berechnung zeitlich lange genug fortgesetzt wird, zeigt sich, dass es im hinteren Bereich des Berechnungsgebietes periodisch immer wieder zum Aufwallen von Turbulenzflecken kommt.

Einschränkend muss angemerkt werden, dass das Turbulenzmodell für die Berechnung von kleinen turbulenten REYNOLDS-Zahlen nicht geeignet ist. In diesem weitgehend abgeklungenen Zustand unterschreiten die Turbulenzgrößen bereits die Clipping-Grenze (s. Abschnitt 8.3.2) und sind daher unrealistisch. Die Vorgabe der konstanten Turbulenzgrößen an der Sohle steht nicht in Übereinstimmung mit der nachlassenden Sohlschubspannung, die als Folge der abklingenden Turbulenz angenommen werden muss. Bei einer Verfeinerung des Zeitschritts von 50 s auf 5 s zeigt sich, dass der wieder aufwallende Turbulenzfleck flacher ist. Aus Gründen der Anschaulichkeit wird aber in Bild 42b die Berechnung mit dem Zeitschritt t=50 s wiedergegeben. Entfernt errinnert der Turbulenzfleck an die kohärente Struktur, die von NEZU und NAKAGAWA [89] als ,,bursting`` beschrieben wird. Für die Berechnung von kohärenten Strukturen reicht aber die horizontale Diskretisierung (20 m) nicht aus. Die vertikale Diskretisierung entspricht derjenigen im Beispiel aus Abschnitt 9.3.3.

Trotz einiger Unzulänglichkeiten ist dieser Testfall in diese Arbeit aufgenommen worden, da er deutlich macht, dass bei geringen Fließgeschwindigkeiten, bei denen Deposition erfolgt, der Turbulenzzustand langwellig instationär und leicht störanfällig ist. So ist die turbulente Zeitskala, Gl. (7.9), am Einströmrand oberhalb von 1,5 m Abstand von der Sohle mit 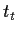= 30 s bereits relativ groß und nimmt mit der abklingenden Turbulenz im weiteren Verlauf der Strömung noch zu. Insgesamt hat die Strömung allerdings eine REYNOLDS-Zahl von Re=3,2. Für die Abkopplung der oberen Wasserschichten von der Sohlreibung ist die langsame Informationsübertragung in vertikaler Richtung verantwortlich, siehe dazu auch die Bemerkung zu internen Grenzschichten in Abschnitt 6.8.

Dieser Testfall hat die Kennung ,,deposi`` in der bereits angegebenen Quelle http://www.wyrwa.de/casu/test.

folgt: 10. Auswertung hinauf: 9.5 Suspendierte Sedimente vorher: 9.5.2 Erosion